Entropy and Information Gain

This is mostly based PowerPoint slides written by Andrew W. Moore of Carnegie Mellon University

http://www.autonlab.org/tutorials/infogain.html

Let's say we have a variable X that can have four possible values, A, B, C, and D.

We might see something like BAACACCDDCDADABCDBBB

Where:

Example 1

P(X=A) = 1/4

P(X=B) = 1/4

P(X=C) = 1/4

P(X=D) = 1/4

If we can only encode this data using 0's and 1's (think of Morse code), you can code each value using 2 bits.

Value	Code
A	0 0
B	0 1
C	1 0
D	1 1

What if, as in the English language, all letters are not equal? i.e. different letters appear with different probabilities.

Example 2

P(X=A) = 1/2

P(X=B) = 1/4

P(X=C) = 1/8

P(X=D) = 1/8

Can we invent a code that uses, on average, 1.75 bits?

Value	Code
A	0
B	1 0
C	1 1 0
D	1 1 1

(This code is not unique)

1/2 * 1 + 1/4 * 2 + 1/8 * 3 + 1/8 * 3 = 1.75

What if we had a variable with three equally likely values?

P(X=A) = 1/3

P(X=B) = 1/3

P(X=C) = 1/3

A naïve coding would use 2 bits each value

Value	Code
A	0 0
B	0 1
C	1 0

Can we devise a code that uses only 1.6 bits? (Actually, theoretically we only need 1.58496 bits)

Value	Code
A	0
B	1 0
C	1 1

There is obviously something "mathematical" going on here!!

Let's go back to Example 2.

Example 2

P(X=A) = 1/2

P(X=B) = 1/4

P(X=C) = 1/8

P(X=D) = 1/8

Intuitively speaking, if A occurs half the time, then we need only one bit to code A.

B occurs only 1/4 of the time. Therefore we should need less than 1 bit, proportionally, to represent B.

Where's the math?

The number of bits needed to code value A occurring with a probability of 1/2 is;

bits = - log ₂ p where p is the probability with which a particular value occurs

bits(A) = - log ₂ 1/2 = 1

bits(B) = - log ₂ 1/4 = 2

bits (C) = bits(D) = - log ₂ 1/8 = 3

Substituting to find the average we have:

H(X) = - p_A log ₂ p_A - p_B log ₂ p_B- p_C log ₂ p_C- p_D log ₂ p_D

H(X ) = 1/2 * 1 + 1/4 * 2 + 1/8 * 3 + 1/8 * 3 = 1.75

Therefore values occurring with higher probability are coded with fewer bits.

H(X) is the Entropy of X.

General Case: Given that S is our sample,

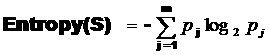
Entropy is a measure of how "mixed up" an attribute is. It is sometimes equated to the purity or impurity of a variable.

High Entropy means that we are sampling from a uniform (boring) distribution. Would have a flat histogram, therefore we have an equal chance of obtaining any possible value.

Low Entropy means that the distribution varies, it has peaks and valleys. The histogram of frequency distribution would have many lows and maybe one or two highs. Hence it is more predictable.

Entropy is a measure of how pure or impure a variable is.

Birdie seed example. A BagA that is equal peanuts and sunflower seeds.

A BagB that has a few peanuts and is mostly sunflower seeds.

BagB has low entropy, BagA has high entropy. We can easier make a decision as to what seed we would most likely pull out of BagB.

Entropy ranges from 0 (all instances of a variable have the same value) to 1 (equal number of instances of each value)

How can we predict output Y given input X.

Example 3

Outlook	Play Tennis
Sunny	No
Sunny	No
Overcast	Yes
Rain	Yes
Rain	Yes
Rain	No
Overcast	Yes
Sunny	No
Sunny	Yes
Rain	Yes
Sunny	Yes
Overcast	Yes
Overcast	Yes
Rain	No

P(Play Tennis = Yes) = 9/14

P(Play Tennis = No) = 5/14

Entropy(Play Tennis) = - 9/14 log ₂ (9/14) - 5/14 log ₂ (5/14) = .940

Suppose we try to predict output of Play Tennis based on an input of Outlook. In other words, knowing the value of Outlook can I decide whether or not to play tennis?

S_rain = [3+, 2-]

P(Outlook = Rain and Play Tennis = yes) = 3/5

P(Outlook = Rain and Play Tennis = no) = 2/5

= .971