1. Summertime approaches! After this semester's Artificial Intelligence course, brain power has gone to an all time low. You decide to give your brain a rest for the summer and let your computer "think" for you. Your first decision each morning is whether or not to go to the beach. You decide to program your computer, using decision trees, so that it can make this all important decision for you. Monitoring your daily beach activity results in the following set of training examples:
|
Day |
Outlook |
Temperature |
Humidity |
Wind |
Go to beach? |
|
D1 |
Sunny |
Hot |
High |
Weak |
Yes |
|
D2 |
Sunny |
Hot |
High |
Strong |
Yes |
|
D3 |
Overcast |
Hot |
High |
Weak |
Yes |
|
D4 |
Rain |
Mild |
High |
Weak |
No |
|
D5 |
Rain |
Cool |
Normal |
Strong |
No |
|
D6 |
Rain |
Cool |
Normal |
Weak |
No |
|
D7 |
Overcast |
Cool |
Normal |
Strong |
No |
|
D8 |
Sunny |
Mild |
High |
Strong |
Yes |
|
D9 |
Sunny |
Cool |
Normal |
Weak |
Yes |
|
D10 |
Rain |
Mild |
High |
Strong |
No |
|
D11 |
Overcast |
Hot |
High |
Strong |
No |
a) (4 points) Given the following formula for Entropy, replace the variables (pi ) in the equation with their appropriate values as given by the above table.
![]()
b) (5 points) If Entropy (S) = .994 and the formula for Information Gain is:
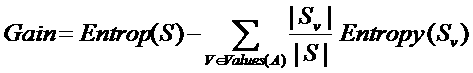
Entropy(Sunny) = 0
Entropy(Overcast) = .918
Entropy(Rain) = 0
What is the Information Gain for the attribute Outlook?
c) (3 points)You calculated the information Gain for each attribute and got the following results:
Gain (S, Humidity) = .151
Gain (S, Wind) = .048
Gain (S, Temperature) = .029
Gain (S, Outlook) = what you calculated in b
Which attribute labels the root node of the decision tree?
d) (5 points)The resulting decision tree is shown below.
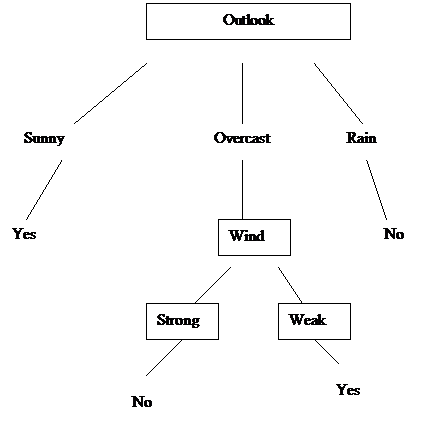
What are the rules for deciding whether or not to go to the beach?
2. (15 points) A perceptron is given the following set of training examples.
|
x1 |
x2 |
result |
|
0 |
0 |
0 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
1 |
1 |

The equations for the Perceptron training rule is:
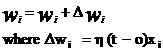
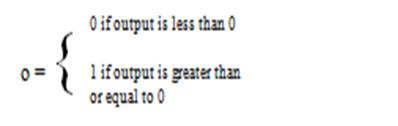
If h = .1 what are the values for w0 , w1 , w2 after one iteration of the perceptron training algorithm?
3. (6 points) Given the following simple two layer feed forward neural network, with two input, two hidden units and one output node, determine the output of the network if the weights are equal to the following values. The threshold function used by each unit is tanh. You only need to set up the equations. Do not solve them.
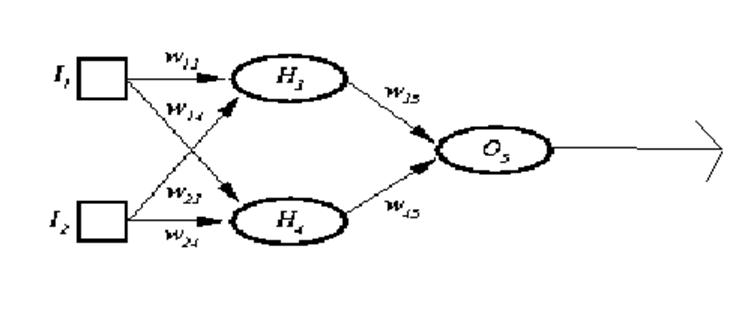
W13 = .4
W14 = .6
W23 = .3
W24 = .4
W35 = .4
W45 = .5
4. The 4 queens problem can be solved using a genetic algorithm. We can represent the 4X4 chess board as a 4 element array with each cell containing the position of the queen in that column. For example, the array 4 1 3 4 represents the placement of queens as follows:
|
|
Q |
|
|
|
|
|
|
|
|
|
|
Q |
|
|
Q |
|
|
Q |
If the population has the following 4 individuals:
Individual A 4 1 3 4
Individual B 4 2 2 1
Individual C 3 4 1 3
Individual D 2 4 1 1
Which individuals survive into the next generation if we end up with the same number of individuals (4)?
- The fitness function you should use is the number of queens that are "safe", i.e. not being attacked, with an evaluation of 4 for the goal configuration. For example the fitness function for 4 1 3 4 evaluates to 1, since only the queen in the second column is safe. Hence 4 2 2 1 evaluates to 0, 3 4 1 3 evaluates to 0, and 2 4 4 1 evaluates to 2.
- Crossover occurs after the between queens (positions) 2 and 3
- There is no mutation
- Individual A mates with Individual B
- Individual C mates with Individual D
5. We
wish to send a message to our mothers (Mom's day is Sunday) expressing our
love, but we have almost no minutes left on our cell phone. Therefore we have to send the shortest
message possible.
Let's
say our messages are coded by a variable
X having five possible values, A, B, C, and D, and E
Where:
|
P(X=A)
= 1/4 |
P(X=B)
= 1/8 |
P(X=C)
= 3/32 |
P(X=D)
= 1/2 |
P(X
= E) = 1/32 |
6
If :
bits
(A) = - log 2 1/4 = 2
bits
(B) = - log 2 1/8 = 3
bits
(C) = - log 2 3/32 = 3.4 which since we can't send a piece of a bit,
is 4.
bits
(D) = - log 2 1/2 = 1
bits
(E) = - log 2 1/32 = 5
a) (2 points) Find H(X), the average number of bits for each message.
b) (1 points) What is another
name for H(X)?
c) (2 points) Create a code for
the above values.
|
Value |
Code |
|
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
|
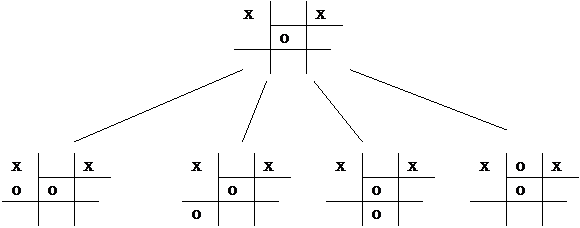
6. Tic tac toe is a children's game that is played as follows:
- One person is X the other is O
- X goes first
- Each person takes turns writing his mark on a 9 square playing board
- The person to be first to display 3 of his marks in a row wins.
Assume we are playing tic tac toe. The diagram shows the current state of the game. It is O's move. He is using minimax search to decide which path to choose in the game tree.
O is a maximizing player
Taking into account symmetry, there are only 4 possible moves O can make
The evaluation function that O uses is:
E(n) = O(n) - X(n)
where O(n) stands for O's possible winning lines
and X(n) stands for X's possible winning lines
a) (8 points) Calculate the evaluation function to each of O's possible moves.
b) (2 points) Which choice does O make based on this evaluation function?
c) (2 points) Is this a good evaluation function? Why or why not? Is there a better move for O than the one minimax picks?