What strategies do computers use in game playing?

Game - competitive environment where agent's goals are in conflict. Results in an adversarial search problem.

Mathematical game theory - any multi agent environment can be viewed as a game provided the impact5 of each agent on the others is "significant "regardless of whether they cooperate or are competitive.

AI games incorporate the game theory definition but are more restricted. AI problems usually deal with deterministic turn taking two player, zero-sum games of perfect information.

What does this mean? We have a deterministic, fully observable environment with two agents whose actions alternate. The utility values of each agent at the end of the game are always equal and opposite One person wins with a value of +1 and the other looses with a value of -1

Why are AI researchers interested in games??

Games are usually too hard to solve.

Ex. chess

a) average branching factor ~35

b) In an average game each player may make about 50 moves

c) To look at the entire search tree we have to examine 35¹⁰⁰ positions

d) if we were to do straight forward search, the first move would not be able to be selected during the lifetime of the opponent!!!

Games are thought to require intelligence!!!!

Two person games - search tree becomes exponentially larger if we add more opponents.

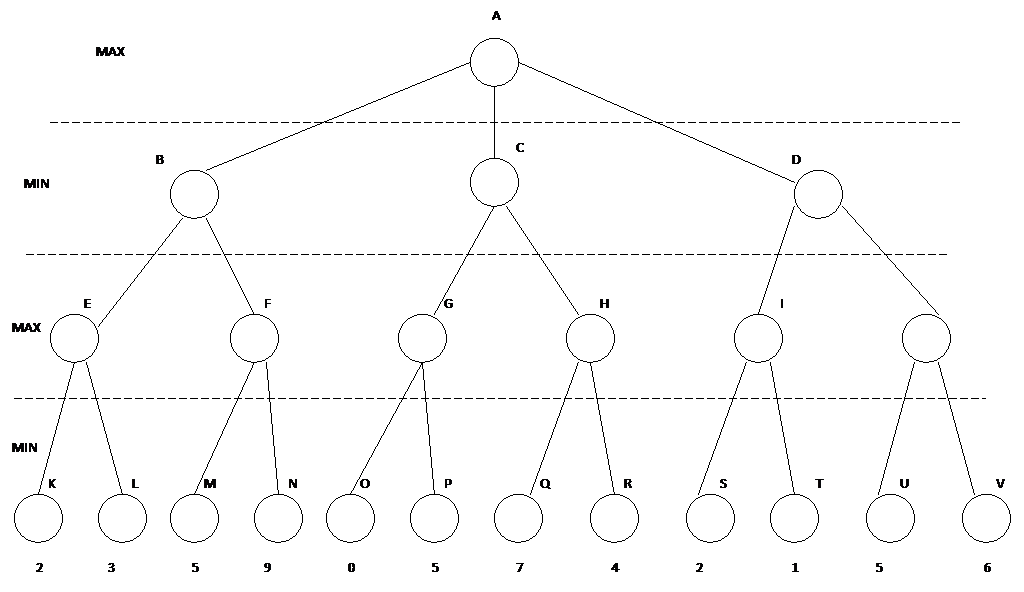
Games are represented by game trees.

Each node in the tree represents a board position.

The ply of a game tree p is the number of levels of the tree, including the root level. If depth = d, then p = d + 1.

In games like chess, a move is a player's choice and its opponents reaction to that choice. Hence a move is 2 ply.

Since exhaustive search is not possible we have to find some strategy that will lead to a win (or less of a loss if points are involved) state for a particular player.

Solution - search to a set depth . Use some kind of evaluation function (heuristic) that will tell you which path to choose from your current position. Your choices are different from your opponent's. you may want to maximize this function while your opponent wishes to minimize it.

Minimax Algorithm

1. Generate game tree to a certain depth.

2. Apply evaluation function to terminal nodes.

3. The evaluation value of the terminal nodes is used to determine the evaluation of the parent node.

4. If the parent node is a maximizer then its value is the maximum evaluation value of its children

5. A minimizer takes the minimum evaluation value of its children

An example of an evaluation function would be piece capture (#pieces captured)

material value - each piece is scored depending on their importance

Evaluation is based on who has more points, min or max

tic tac toe

E(n) = M(n) - O(n)

M(n) - my possible winning lines

O(n) - opponents possible winning lines.

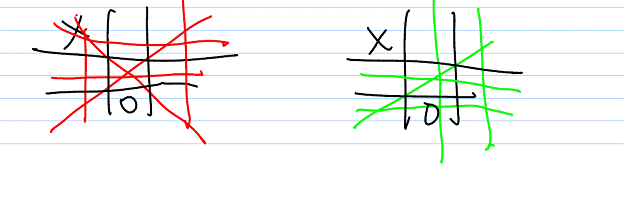
X winning paths = 6 (me)

O winning paths = 5 (opponent)

E(n) = 6 - 5 = 1

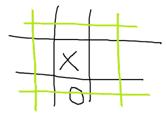X winning paths = 6 (me)

O winning paths = 4 (opponent)

E(n) = 6 - 4 =2 X will prefer this move over the above move

What if, as in chess, moves are timed?

If we go too deep, we won't finish our search in time

If we don't go deep enough, we won't have the "best picture"

Solution - iterative deepening

1) We saw that the # of nodes repeated is small compared to the # of nodes in the deepest level repeated.

2) When time is up, we use the last completed search

In minimax search, need we search the entire search tree?

If a path is going to lead to a bad situation, why bother to evaluate it?

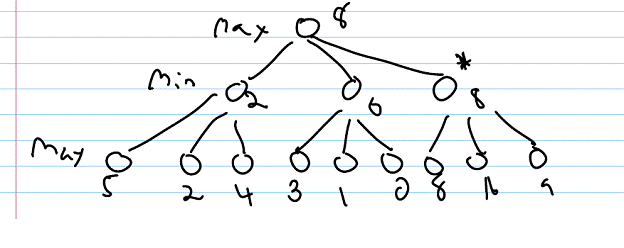
max

min

max

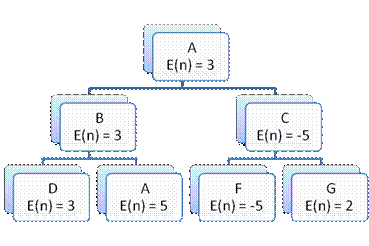
Why bother looking at G when we know that at C, min can do at least -5? No matter what value is at G, max will choose B. Hence we can prune the tree at C.

Minimax With α - β Pruning

1. Descend, doing depth first search, full ply, and apply the evaluation function to the siblings of a state, if these siblings are terminal nodes.

2. If these terminal nodes are MIN nodes then the maximum of these nodes is backed up to their parent, a MAX node. The value is then assigned to the grandparent as a potential β cutoff.

3. If these terminal nodes are MAX nodes then the minimum of these nodes is backed up to their parent, a MIN node. The value is then assigned to the grandparent as a potential α cutoff.

4. We continue the search to the grandchildren of the node.

5. Search is stopped below a MIN node having a β value less than or equal to the α of any of its MAX ancestors.

6. Search is stopped below a MAX node having an α value greater than or equal to the β of any of its MIN ancestors.